記事を読む前に!実践・過去問チャレンジ
電気工事士の筆記試験で、多くの人がつまずきやすいのが計算問題です。特に電線の抵抗に関する問題は、公式を丸暗記しようとすると単位変換や複雑な分数計算でミスをしがちです。
しかし、実はこのタイプの問題は、電線の「ある3つの法則」さえイメージできれば、複雑な計算なしで解くことができます。
まずは、実際に出題された過去問をベースにした問題に挑戦して、現在の理解度をチェックしてみましょう。
【問題】
A、Bの2本の同材質の銅線がある。
Aは直径1.6mm、長さ40m、
Bは直径3.2mm、長さ20mである。
このとき、Aの抵抗はBの抵抗の何倍か。
- 2
- 4
- 6
- 8
答えは決まりましたか?
「直径が半分だから抵抗は2倍?」「長さが2倍だから…」と頭の中で数字がぐるぐるしていませんか?
この問題を解くカギは、電線を「水が流れるホース」に置き換えて考えることです。
正解と、計算ミスをゼロにする解き方を解説します。
1. ズバリ、正解は?
正解は、選択肢の 4(8倍) です。
もし不正解だったとしても安心してください。ここで解説する「比率の考え方」を身につければ、このパターンの問題はすべて得点源に変わります。
2. 公式より簡単!「水とホース」でイメージする
電線の抵抗(電気の流れにくさ)は、難しい公式を使わなくても、直感的に理解できます。電線を「水が流れるホース」だと思ってください。
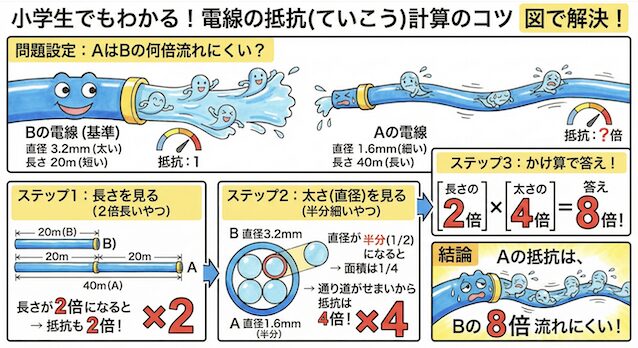
法則1:長さが長いほど、抵抗は大きくなる(比例)
長いホースと短いホース、どちらが水を通すのが大変でしょうか?
当然、長いホースの方が摩擦が増えて水は流れにくくなりますね。
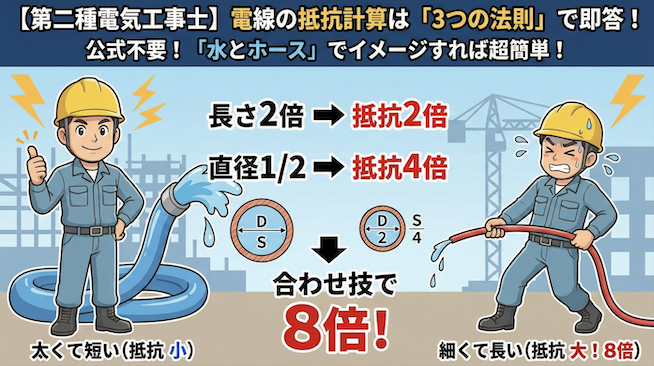
つまり、「長さが2倍になれば、抵抗も2倍」になります。
法則2:太いほど、抵抗は小さくなる(反比例)
太いホースと細いホース、どちらが大量の水を流せますか?
太い方がスムーズに流れます。つまり、太ければ太いほど抵抗は小さくなります。
具体的には、「断面積が2倍になれば、抵抗は半分(1/2)」になります。
法則3:ここが最大の罠!「直径」と「断面積」の関係
試験で最も間違えやすいのがここです。
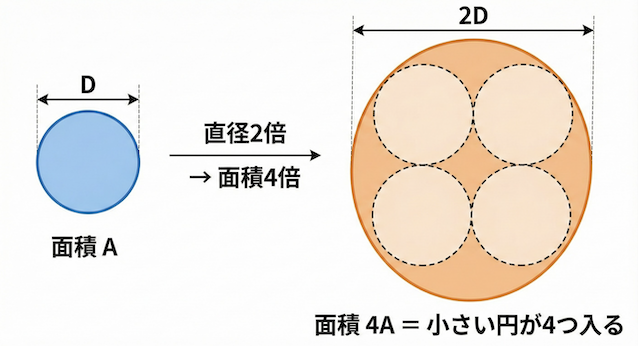
「直径」が2倍になると、「断面積」は何倍になるでしょうか?
円の面積の公式を思い出してください。(半径×半径×3.14)
直径が2倍になると、面積は「4倍」になります。
面積が4倍ということは、抵抗は「1/4」になります。
ここまでのルールを整理しましょう。
- 長さが2倍 → 抵抗は 2倍
- 断面積が2倍 → 抵抗は 1/2倍
- 直径が2倍 → 抵抗は 1/4倍
3. 問題の解説:AはBの何倍か?
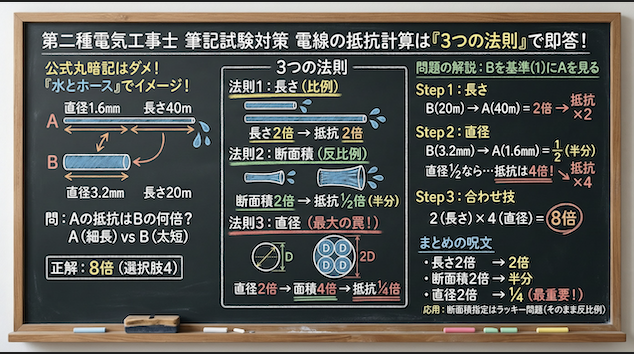
では、先ほどの法則を使って問題を解いていきましょう。
求めたいのは「A(細くて長い)は、B(太くて短い)の何倍の抵抗か?」です。
Bを基準(1とおく)にして、Aがどう変化しているかを見ていきます。
ステップ1:長さの比較
- 電線B:20m
- 電線A:40m
AはBに比べて、長さが「2倍」です。
長さが2倍なので、この時点で抵抗は「2倍」になります。
(ここまでは簡単ですね)
ステップ2:直径(太さ)の比較
- 電線B:直径3.2mm
- 電線A:直径1.6mm
AはBに比べて、直径が「半分(1/2)」になっています。
ここがポイントです。「直径が半分」になると、抵抗はどうなるでしょうか?
先ほどの法則の逆を考えます。
「直径が2倍なら抵抗は1/4」でした。
逆に「直径が1/2(細くなる)」なら、抵抗は「4倍」になります。
(細いストローほど飲み物を吸うのに力がいるイメージです)
ステップ3:合わせ技一本
最後に2つの要素を掛け合わせます。
- 長さが2倍になったことで、抵抗は 2倍 になった。
- 直径が半分になったことで、抵抗は 4倍 になった。
これらを掛け合わせると…
2 × 4 = 8
答えは「8倍」となります。
4. 他のパターンの攻略法(応用編)
この問題には、少し形を変えた類題も存在します。しかし、基本の考え方は同じです。
パターンA:断面積で出題された場合
「断面積5.5mm2」のように、直径ではなく最初から断面積が書かれている問題もあります。
この場合はラッキー問題です。
「断面積が半分なら、抵抗は2倍」とシンプルに反比例させるだけでOKです。直径のように2乗する必要はありません。
パターンB:抵抗値を等しくしたい場合
「AとBの抵抗を同じにするには、長さをどうすればよいか?」といった問題です。
今回の場合、AはBの8倍も抵抗がありました。
抵抗を同じにするには、Aを短くするか、Bを長くする必要があります。
計算等のロジックは同じで、「今の抵抗倍率」を出してから、それを打ち消す長さを考えれば正解にたどり着けます。
まとめ
電線の抵抗問題は、まともに抵抗率の公式を使って計算すると、時間がかかる上に計算ミスのリスクが高まります。
以下の3つの呪文を覚えて、サクサク解いてしまいましょう。
- 長さ が2倍なら、抵抗は 2倍 (素直に比例)
- 断面積 が2倍なら、抵抗は 半分 (素直に反比例)
- 直径 が2倍なら、抵抗は 1/4 (2乗に反比例!)
特に3つ目の「直径」のルールは、第二種電気工事士試験で繰り返し問われる最重要ポイントです。これさえ押さえておけば、この分野は合格への大きな得点源になります。