記事を読む前に!実践・過去問チャレンジ
第二種電気工事士の試験勉強で、多くの人がつまずいてしまうのが「電気の基礎理論」です。特に交流回路におけるコイル(インダクタンス)やコンデンサの計算問題は、単なるオームの法則だけでは解けないため、苦手意識を持つ方も多いのではないでしょうか。
しかし、この分野は「周波数と電流の関係」というたった一つのルールさえ理解していれば、実は複雑な公式を使わなくても解ける問題が少なくありません。
今回は、コイルの回路において「周波数が変化したとき、電流はどうなるか?」を問う問題です。
試験本番で確実に点数を取るために、まずは今の実力をチェックしてみましょう。
【問題】
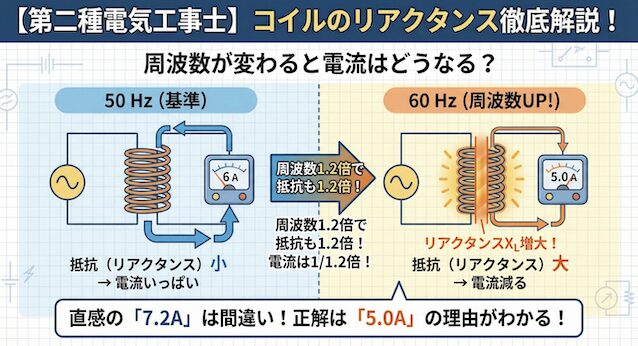
図のような交流回路において、周波数 50 Hz の正弦波交流電圧を加えたとき、電流計の指示値は 6 A であった。
電圧を変えずに、電源の周波数を 60 Hz にしたとき、電流計の指示値 [ A ] はいくらか。
ただし、コイルの抵抗は無視できるものとする。
- 4.0
- 5.0
- 6.0
- 7.2
答えは決まりましたか?
「周波数が上がったのだから、電気もたくさん流れるのでは?」と直感で「7.2 A」を選んでしまった方は要注意です。
コイルという部品が交流に対してどのような性質を持っているか、その仕組みを正しく理解することが合格への近道です。
1. ズバリ、正解は?
正解は、選択肢の 2(5.0) です。
なぜ周波数が上がると電流が減ってしまうのか。その理由と、試験中に電卓を使わずとも暗算で解けるような考え方を解説します。

2. 解説:コイルは「変化」を嫌うあまのじゃく
この問題を解くために必要な知識は、大きく分けて2つあります。
ポイント1:誘導性リアクタンス(交流の抵抗)
交流回路にコイルをつなぐと、コイルは電流の変化を妨げようとする「抵抗」のような働きをします。この電流の流れにくさを「誘導性リアクタンス」と呼び、単位は抵抗と同じオーム [ Ω ] を使います。
誘導性リアクタンス XL は、次の式で表されます。
XL = 2πfL
- f :周波数 [ Hz ]
- L :インダクタンス [ H ]
この式で最も重要なのは、「誘導性リアクタンス(抵抗の大きさ)は、周波数に比例する」という点です。
周波数が高くなればなるほど、コイルの抵抗成分は大きくなります。
イメージとしては、コイルは「変化を嫌う」性質を持っています。
周波数が高い(=変化が激しい)電気が来ると、コイルは強く反発して通そうとしません。逆に、周波数が低い(=変化が緩やかな)電気はスムーズに通します。
ポイント2:周波数と電流の計算
今回の問題では、周波数が 50 Hz から 60 Hz に変化しました。
倍率で考えると、以下のようになります。
60 ÷ 50 = 1.2 倍
周波数が 1.2 倍になると、コイルの抵抗(誘導性リアクタンス)も比例して 1.2 倍になります。
抵抗が大きくなれば、当然、流れる電流は減ります。
オームの法則(電流 = 電圧 ÷ 抵抗)の関係から、電流は抵抗に反比例するため、計算は以下のようになります。
元の電流 6 A ÷ 1.2 = 5 A
よって、電流は 5.0 A になります。
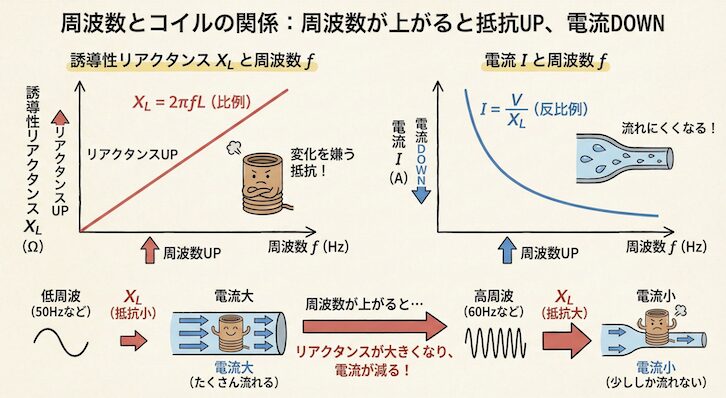
「コイルの場合、周波数が上がると電流は減る」
この結論だけでも覚えておけば、選択肢の 3(変化なし)や 4(増加)を瞬時に除外でき、正解率がぐっと上がります。
3. もう一つの重要知識「位相の遅れ」
コイルの回路については、計算問題だけでなく、電圧と電流のタイミング(位相)に関する知識問題も頻出です。
以下のルールもあわせて覚えておきましょう。
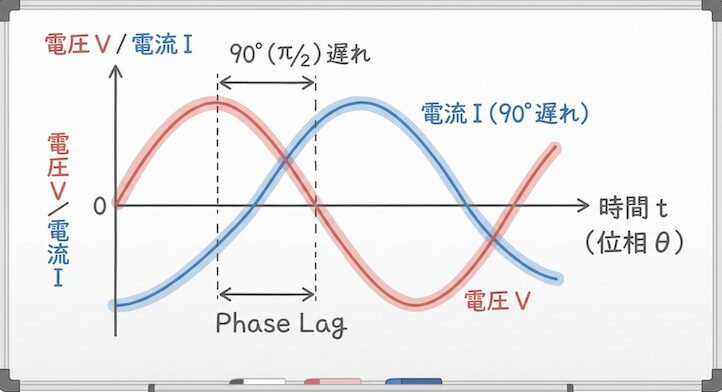
「コイルに流れる電流は、電圧よりも位相が 90 度遅れる」
コイルは変化を嫌う性質があるため、電圧がかかっても、ワンテンポ遅れてから電流が流れ始めるとイメージしてください。
ちなみに、コンデンサの場合は逆で、電流が 90 度「進み」ます。
どっちがどっちか分からなくなったときは、「コイル(L)は、遅れる(Late)」と、英語の頭文字で関連付けて覚えるのがおすすめです。
まとめ:この問題の攻略ポイント
- コイルの抵抗成分(誘導性リアクタンス)は、周波数に比例する。
- 周波数が高くなると、コイルは電気を通しにくくなる(電流は減る)。
- 計算時は、周波数が何倍になったかを確認し、電流値をその倍率で割る。
- コイルの電流位相は、電圧より 90 度遅れる。
電気工事士の試験では、複雑な数式計算よりも、このような「比例・反比例の関係」や「素子の性質」を理解しているかを問う問題が多く出題されます。
一つひとつの法則を丁寧に押さえて、確実に得点につなげましょう。