記事を読む前に!実践・過去問チャレンジ
電気工事士の筆記試験において、「電気基礎理論」は最初の鬼門になりがちです。
特に、数式が並ぶ計算問題を見ると「難しそう……」と後回しにしてしまう人も多いのではないでしょうか。
しかし、今回解説する「電線の抵抗率」を求める問題は、一度理屈を理解してしまえば、数字が変わるだけのパターン問題として得点源にできます。
平成26年、令和3年、令和6年と繰り返し出題されている頻出問題です。まずは力試しをしてみましょう。
【問題】
電気抵抗 R [Ω]、直径 D [mm]、長さ L [m] の導線の抵抗率 [Ω・m] を表す式はどれか。
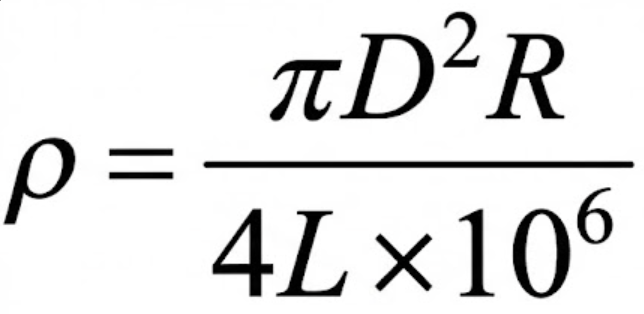
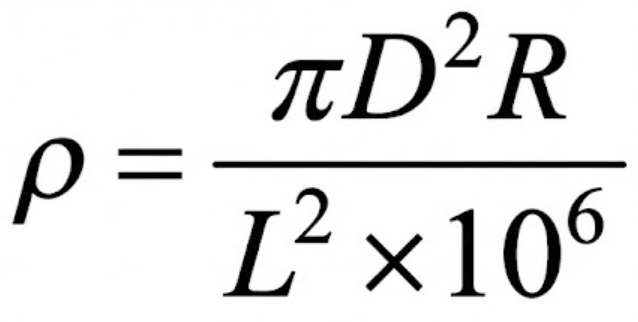
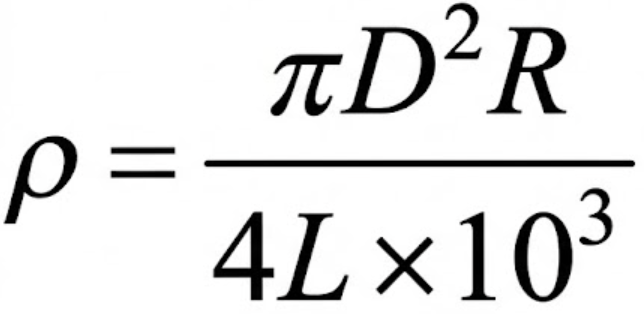
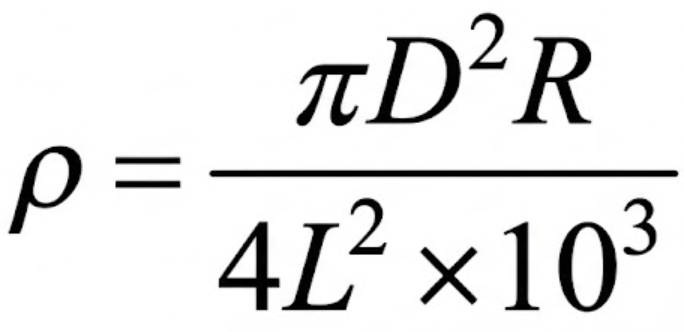
答えは決まりましたか?
選択肢を見ると、どれも似たような式で迷ってしまいますよね。
特に分母にある「10の6乗」や「10の3乗」といった数字。これがどこから来たのかを理解することが、この問題を解くカギになります。
それでは、正解と詳しい解説を見ていきましょう。
1. ズバリ、正解は?
正解は、選択肢の 1 です。
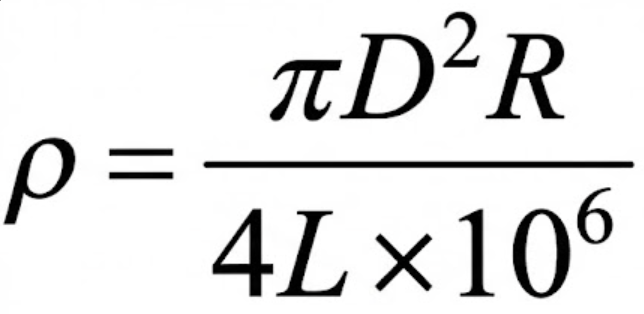
なぜこの式になるのか、順を追って解説します。
丸暗記しようとすると、Lが2乗だったか、10の3乗だったかと試験本番で混乱してしまいます。
「なぜそうなるのか」という導き方を覚えるのが合格への近道です。
2. 解説:3つのステップで式を導こう

この問題を解くには、以下の3つの要素を理解する必要があります。
- 基本の抵抗の公式
- 断面積の求め方(直径から面積へ)
- 単位変換(mm2 から m2 へ)
ひとつずつ紐解いていきましょう。
ステップ1:基本公式を思い出す
まず、電線の抵抗 R を求める基本の公式は以下の通りです。
「抵抗は長さに比例し、断面積に反比例する」という法則ですね。
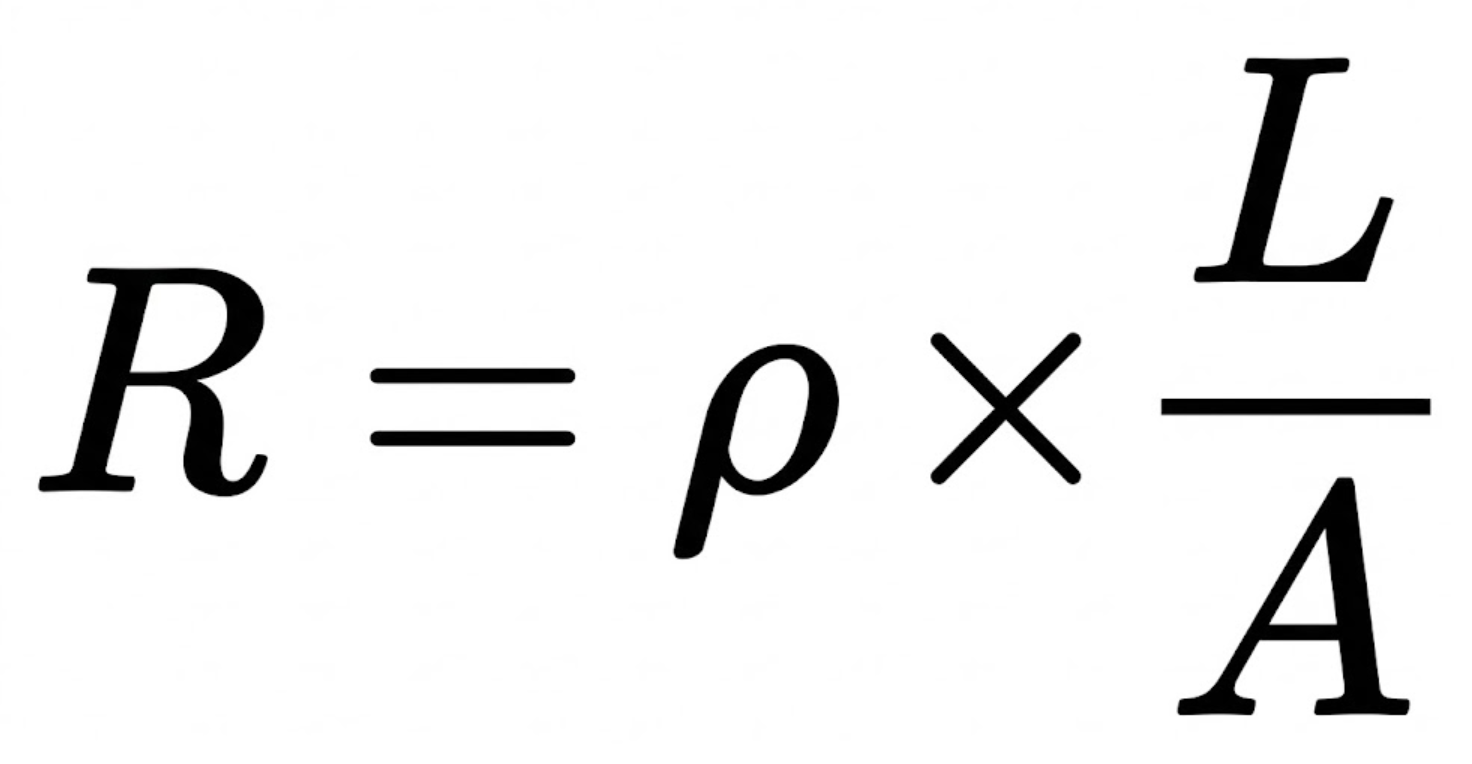
- R:電気抵抗 [Ω]
- ρ(ロー):抵抗率 [Ω・m]
- L:長さ [m]
- A:断面積 [m2]
今回は「抵抗率 ρ」を求める問題なので、この式を ρ = の形に変形しておきます。
両辺に A/L を掛けると、ρ だけが残ります。
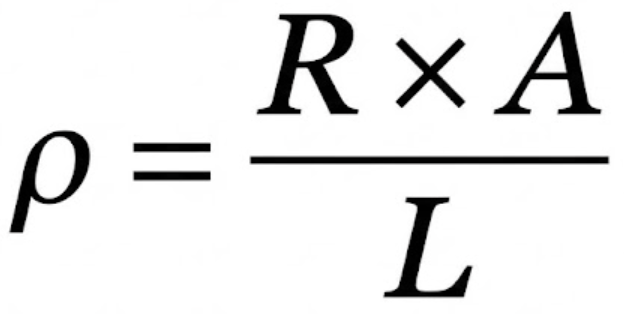
ステップ2:断面積 A を直径 D で表す
問題文には「断面積 A」ではなく、「直径 D」が与えられています。
円の面積を求める公式を思い出しましょう。半径を r とすると πr2 ですね。
直径 D を使うと、半径は D/2 なので、断面積 A は以下のようになります。
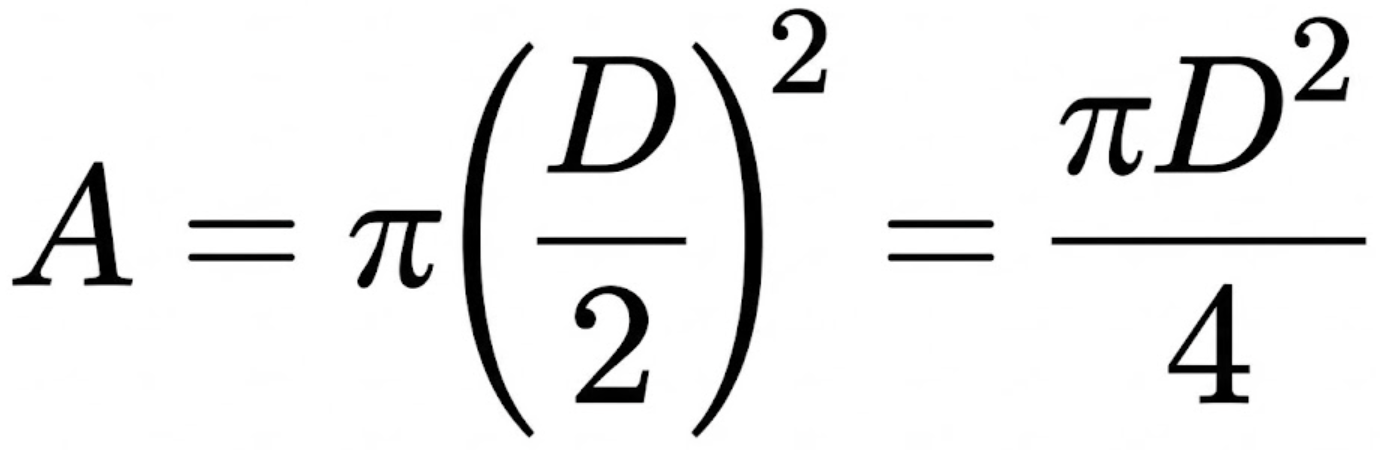
これをステップ1の式に代入すれば良さそうですが、ここで【最大の落とし穴】があります。
ステップ3:単位の罠「10の6乗」を攻略する
ここがこの問題の一番のポイントです。単位をよく見てください。
- 問題文の直径 D の単位は【mm】
- 抵抗率の単位は【m】
公式の中で計算するには、単位を【m】(メートル)に統一しなければなりません。
面積の単位である [mm2] を [m2] に直す必要があります。
- 1 m = 1000 mm
- 1 m2 = 1,000,000 mm2 (1000 × 1000)
つまり、1 mm2 は 1 m2 の100万分の1です。
数式で書くと、「10のマイナス6乗」を掛けることになります。
![]()
先ほど求めた断面積の式に、この単位変換を適用します。
ステップ4:式を組み立てる
準備は整いました。
ステップ1で作った式に、単位変換した断面積を代入します。
- 分子には、円周率 π、直径 D の2乗、抵抗 R が乗ります。
- 分母には、半径計算で出た 4 と、長さ L が来ます。
- そして、単位変換のための 10の6乗 が分母に来ます。
数式を整理すると、以下のようになります。
(分子にある10のマイナス6乗は、分母の10のプラス6乗と同じ意味です)
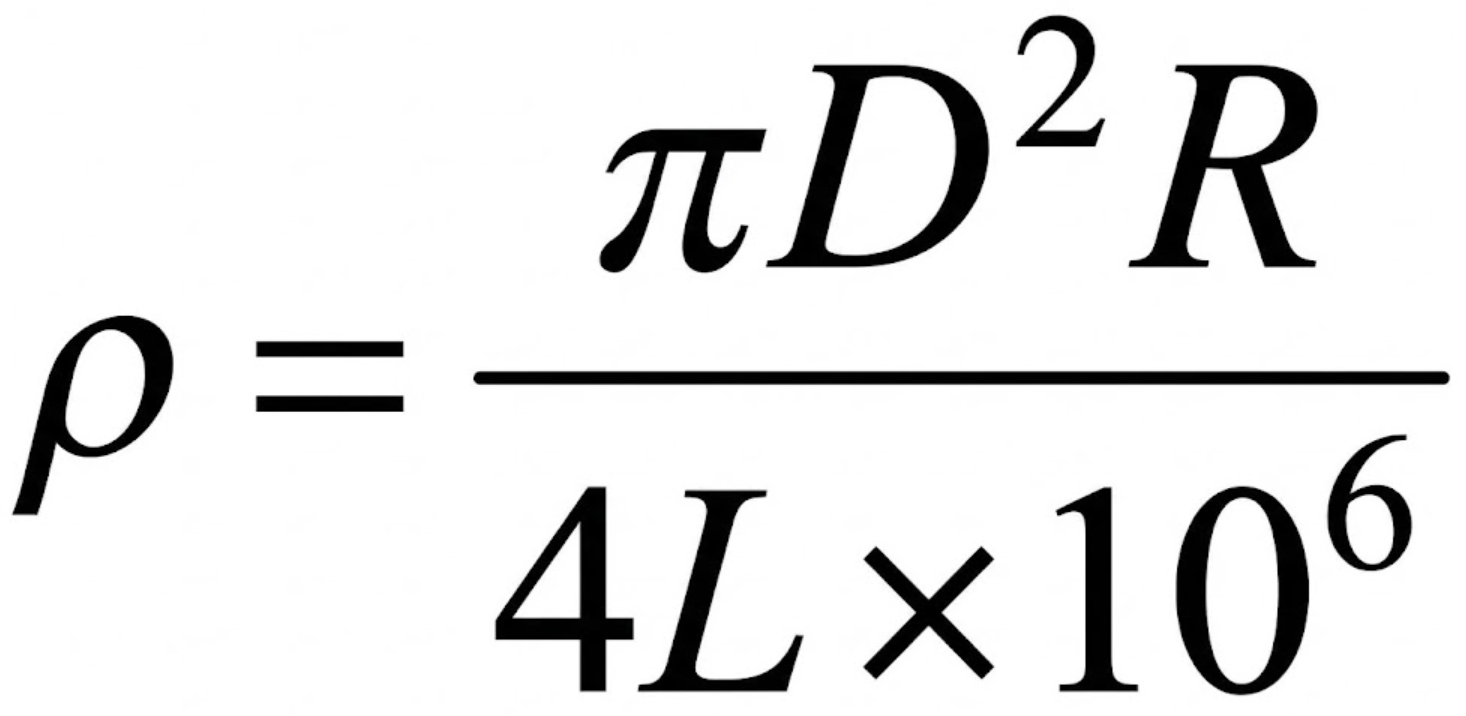
これが選択肢 1 の形と一致します。
3. 覚え方のコツ
試験本番で迷わないために、以下のポイントをチェックしてください。
- 【Dは2乗か?】面積の計算なので、直径 D は必ず2乗になります。
- 【分母に4があるか?】半径(D/2)を2乗するので、分母に4が出てきます。
- 【分母に10の6乗があるか?】mm を m に直して2乗するので、0が6個分の補正が必要です。
まとめ
この問題が出たら、まずは分母に「10の6乗」がある選択肢を探しましょう。それだけで選択肢を絞り込むことができます。
電気工事士の試験では、このように「単位」や「公式の変形」を問う問題がよく出ます。
丸暗記ではなく理屈を一度納得しておけば、試験当日にド忘れしても自分で式を導き出すことができますよ。



