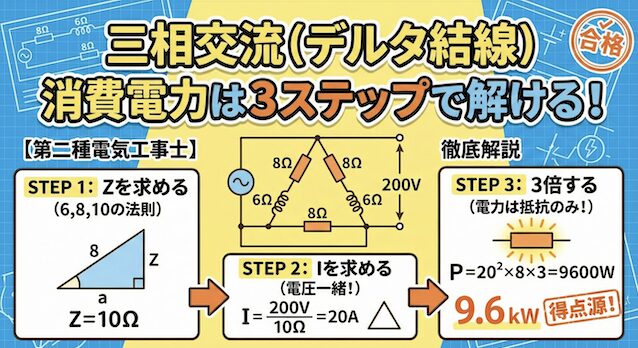
記事を読む前に!実践・過去問チャレンジ
筆記試験の勉強を進める中で、三相交流回路の計算問題を見て「難しそう」とページを飛ばしていませんか?
ルート(√)が出てきたり、回路が複雑に見えたりして敬遠されがちですが、実は「出題パターンが決まっている」ため、一度解き方を覚えてしまえば確実な得点源になる問題です。
今回は、令和元年、令和4年、令和5年と繰り返し出題されている「デルタ結線」の消費電力を求める問題を解説します。
公式を丸暗記するのではなく、電気の流れをイメージしながら解いてみましょう。
【問題】
図のような三相3線式回路の全消費電力[kW]は。
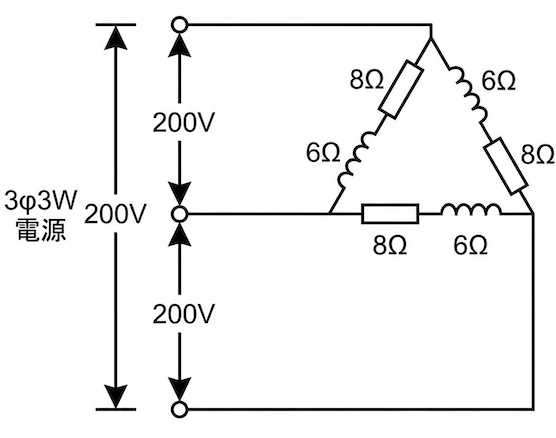
- 2.4
- 4.8
- 9.6
- 19.2
答えの予想はつきましたか?
「電圧が200Vで抵抗が8Ωだから……」といきなり計算を始めると、思わぬ落とし穴にはまるかもしれません。
三相交流回路には、単相回路とは違う「電圧と電流のルール」があります。
自信を持って「これだ!」と選べるように、順を追って解説していきます。
1. ズバリ、正解は?
正解は、選択肢の 3(9.6) です。
計算過程で数値が大きくなるため不安になったかもしれませんが、単位が [W] ではなく [kW] であることに注意すれば正解にたどり着けます。
では、なぜ「9.6」になるのか、3つのステップで攻略していきましょう。
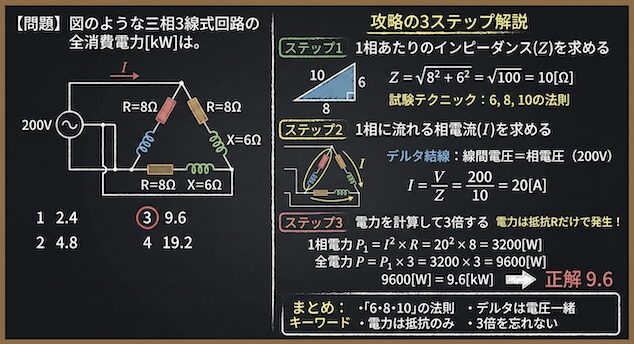
2. 攻略の3ステップ解説
三相交流(特にデルタ結線)の消費電力を求める問題は、回路全体を一気に考えるのではなく、「1つの相(三角形の1辺)」だけを取り出して考えるのが鉄則です。
ステップ1:1相あたりの「インピーダンス(Z)」を求める
まずは、三角形(デルタ)の1辺にある「抵抗 8Ω」と「コイル(リアクタンス)6Ω」の合成抵抗、すなわちインピーダンス Z を求めます。
抵抗とコイルは性質が違うため、単純な足し算(8 + 6 = 14)はできません。直角三角形を用いた「三平方の定理」を使います。
Z = √(R^2 + X^2)
数字を当てはめると:
Z = √(8^2 + 6^2) = √(64 + 36) = √100 = 10 [Ω]
これで、1つの相の電気の流れにくさは 10Ω だと分かりました。
<試験テクニック>
「6」と「8」の組み合わせが出たら、斜辺(インピーダンス)は「10」になります(3:4:5の直角三角形の2倍)。計算しなくても「10Ωだ!」と即答できるようにしておくと時間を短縮できます。
ステップ2:1相に流れる「相電流(I)」を求める
次に、その1つの相にどれくらいの電流が流れるかを計算します。ここで重要なのが「デルタ結線の電圧ルール」です。
[ 画像差し込み:デルタ結線の電圧・電流関係を示す図。線間電圧=相電圧 であることを強調した図 ]デルタ(Δ)結線では、電線間の電圧(線間電圧)が、そのまま負荷の電圧(相電圧)になります。
つまり、問題文にある 200V が、そのまま抵抗とコイルにかかります。
(スター結線のようにルート3で割る必要はありません)
オームの法則(I = V / Z)を使って電流を求めます。
I = 200 / 10 = 20 [A]
1つの相には 20A の電流が流れていることが分かりました。
ステップ3:電力を計算して3倍する
最後に消費電力を求めます。ここで一番大切なルールを思い出してください。
「電力(消費電力)は、抵抗 R だけで発生する」
コイル(リアクタンス)では電力は消費されません。ですから、計算に使うのはインピーダンス(10Ω)ではなく、抵抗の 8Ω です。
まず、1相あたりの消費電力 P1 を計算します。
P1 = I^2 × R
P1 = 20^2 × 8
P1 = 400 × 8 = 3200 [W]
これが1相分(1辺分)の電力です。三相回路なので、これが3つ分あります。最後に3倍します。
P = 3200 × 3 = 9600 [W]
問題の単位は [kW] なので、1000で割ります。
9600 [W] = 9.6 [kW]
よって、正解は 3 となります。
まとめ:この問題の攻略キーワード
今回の解法手順を整理します。
- 「6・8・10」の法則:インピーダンス計算を一瞬で終わらせる。
- デルタは電圧一緒:線間電圧 200V = 相電圧 200V。
- 電力は抵抗のみ:電力計算には R(8Ω)を使う。
- 3倍を忘れない:三相なので最後に×3をする。
この手順さえ守れば、数字が変わっても全く同じように解くことができます。
難しいルート3の計算を使わずに、「電流の2乗×抵抗×3」で解くこの方法は、計算ミスも少なくおすすめです。ぜひ得点源にして、合格に近づきましょう。